Google OR-Tools is an open-source suite of tools that grants developers the ability to solve problems using combinatorial optimization. The goal of using Google OR-Tools is to identify a solution to your problem based on your defined parameters.
This could be to discover a single 'best' solution or a workable one that does not violate any of your established requirements. Here at Audacia, we are proud to have contributed an example to their source code as well.
Principal Consultant Owen Lacey has addressed the powerful features of Google OR-Tools in a previous post, where he constructed a simple optimisation model using Google OR-Tools by addressing a classic Vehicle Routing Problem (VRP). This piece addresses three of the most commonly faced combinatorial optimisation problems through the planning of an Audacia office pizza party.
The organisation of the party has been split into three stages: routing, scheduling and assigning. Here is a brief breakdown of each stage:
- Routing: Ensures that employees are all collected and taken to the party. This is a Vehicle Routing Problem. Here we’re looking to minimise the amount of time it takes to go and get all the employees, or the distance travelled to get each employee, depending on how we look at it.
- Scheduling: This stage will involve cooking the pizza, with separate substages including shaping, slicing and preparing. This is a scheduling problem; we need to create a supply chain of pizza making which minimises the amount of time it takes to cook all the pizzas so that they’re cooked as quickly as possible and can be served to our hungry employees.
- Assigning: The final stage involves dishing out our pizza. Crucially, we have not asked everyone what pizza they want, but everyone has a favourite flavour of pizza, which they rate out of 10. We are, therefore, trying to optimise how much everyone likes their assigned pizza.
These rules replicate some of the real parameters that you might potentially set in an optimisation problem like this. Over a series of three blog posts, we will discuss each stage in detail, with code samples and examples of successful unit tests. For part we look at routing; ensuring that everyone is picked up and successfully transported to the party in the most optimised way possible.
1. Routing
For this initial stage we have outlined some ground rules that will inform our code:
- Firstly, the Party is mandatory; everyone must be in attendance (after all, why wouldn’t they want to attend the best pizza party ever?!)
- Cars can use multiple drivers to complete the journeys
What this means is that every node must be visited and, in turn, no nodes are dropped. If you wanted to be able to drop nodes, you must include a penalty to do so. This penalty should reflect how much you want to penalise dropping a node. The higher this penalty, the less inclined the model will be to drop the node. Specific penalties can be applied on a per-node basis, or you can apply a fixed penalty for dropping any given node.
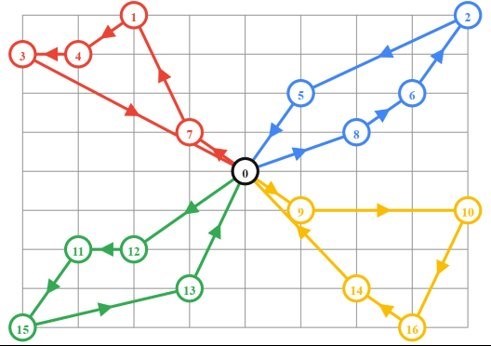
Multiple drivers can be used as well to complete these journeys. The above diagram visualises this through different colour lines. If there was only one driver completing the pick-ups and drop-offs, then all journeys would be displayed in one colour.
Node zero — the black circle in the centre — represents the office which will be the starting point for all the drivers, as well as the drop-off for all employees. Note that the diagram illustrates the shortest overall amount of time it takes to pick up the employees.
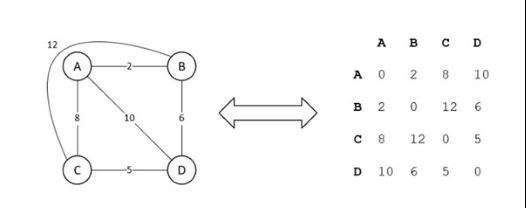
If we consolidate the first diagram with some distances, we get something like this complete graph here. This graph shows that each node is travelable from another node. Much like in a real-life scenario, we can hypothetically travel between any two of our colleagues' houses.
This fact can be further translated to a 2x2 matrix which represents the distance between the two nodes. In this instance, we’ll refer to A as the office, which is node zero. Note that the matrix is symmetrical which means that the distance from A to B is the same as the distance from B to A. Further evidence of this is illustrated in the diagonal line of symmetry in the matrix.
Of course, this isn’t always the case in real life. When focusing on distance, specifically, there can be factors like one-way roads or a dual carriageway which invoke discrepancies in your travel time, i.e., it takes 15 minutes to get to point A from B, but 20 minutes to return to point B.
It does not mean that your matrix always needs to be symmetrical. If you have a matrix of distances, this is how we represent in a way that allows developers to write the information in C#.
1.1. Unit Tests
Before looking at any Google OR-Tools code, we can do some Test-Driven Development to make sure our constraints are covered. Using some code samples, we’ll look at how our rules are translated into C#. Firstly, is our distance matrix:
/// <summary>
/// Symmetric matrix of node distances, of size n+1 x n+1, where n is the number of employees to pick up.
/// </summary>
private read only long[,] _distances =
{
{ 0, 3, 2, 5 },
{ 3, 0, 1, 11 },
{ 2, 1, 0, 10 },
{ 5, 11, 10, 0 }
};
The first rule we defined was that every node was mandatory, which translates to this unit test which outlines that ‘each employee is picked up’. This vehicle routing problem also has a model which takes in a distance matrix with the distances shown above. For example, from the office to the first employee is 3, the office to the second employee is 2 and so forth.
[Fact]
public void Each_employee_is_picked_up()
{
var random = new System.Random();
var employeeNames = new List {random.Forename(), random.Forename(), random.Forename()};
var driverName = random.Forename();
var model = new PickUpEmployeesModel(_distances, employeeNames, new List {driverName});
var solver = new PickUpEmployeesSolver(model);
var assignments = solver.Solve();
assignments[driverName].Should().HaveCount(employeeNames.Count);
}
The concept of Test-Driven Development (TDD) is really useful when you’re using Google OR-Tools as your unit tests and constraints begin to function as acceptance criteria, i.e. each employee must be picked up.
You can write a unit test for each constraint and, crucially, if you’re writing more and more constraints for your model later, it can be easy to unknowingly break the other rules. As is well known with unit testing, covering your constraints with tests provide protection against these scenarios, especially with something that is more complex to manually verify like a Google OR-Tools model.
To solve the model, our solver requires 3 pieces of information:
- The names of the employees to pick up: employeeNames
- The names of the driver(s) to use: driverName
- The distances between our employees’ houses, and to/from the office: _distances
For this unit test, we are using another piece of Audacia open-source code, known as Audacia.Random.
We instantiate our solver and invoke the attempt at finding the optimal solution via `solver.Solve()`. This solver returns a dictionary of driver names to the employees they are picking up. It will only add an element to that dictionary if the driver is picking anyone up, rather than returning an element with no values.
The final line of the code essentially ensures that all the employees are picked up, by stating that the one driver should have a count of employees. Should().BeEquivalentTo(expectedRoute) works off fluid assertions, which means that it will throw in an exception if the request is wrong or is not met.
[Fact]
public void Model_minimizes_distance_travelled()
{
var random = new System.Random();
var employeeNames = new List {random.Forename(), random.Forename(), random.Forename()};
var driverName = random.Forename();
var solver = new PickUpEmployeesSolver(new PickUpEmployeesModel(_distances, employeeNames, new List {driverName}));
var assignments = solver.Solve();
// By inspection, we should go to nodes B -> D -> C.
var expectedRoute = new[] {employeeNames[0], employeeNames[2], employeeNames[1]};
assignments[driverName].Should().BeEquivalentTo(expectedRoute); }
In this test, Model_minimizes_distance_travelled() is just asserting that this is the shortest route travelled. The matrix should validate that this is the shortest distance travelled, i.e. by travelling from B to D to C (employee 1 to employee 3 to employee 2). As mentioned in the test, we can see from this minimal example that this would be the shortest path between the employees. This gives us confidence that when the model attempts to solve something more complex, it will act in the same way.
[Fact]
public void Uses_multiple_cars_if_faster()
{
var random = new System.Random();
var employeeNames = new List {random.Forename(), random.Forename(), random.Forename()};
var firstDriverName = random.Forename();
var secondDriverName = random.Forename();
var driverNames = new List {firstDriverName, secondDriverName};
var solver = new PickUpEmployeesSolver(new PickUpEmployeesModel(_distances, employeeNames, driverNames));
var assignments = solver.Solve();
assignments.Should().HaveCount(driverNames.Count);
}
This test showcases our second rule; multiple cars can be used if this speeds up the overall journey. Crucially, as we have two drivers to use, we provide two driver names for the model to utilise.
The test states that we should use both drivers. The number of elements in the dictionary that we get back is the number of drivers, i.e. we have assigned at least one person to each driver.
1.2. Pick up Employees Solver - Explained
Each unit test shown above instantiates a solver and finds a solution. Here we will look at the Google OR-Tools model implementation the unit tests are covering. The first Google-OR Tools API to use for this problem is the RoutingIndexManager (with the help of C#9’s Target-typed new expressions)
RoutingIndexManager manager = new(_model.DistanceMatrix.GetLength(0), _numberOfCars, 0);
Our manager needs to know how many nodes there are (this is the length of the Distance Matrix and is the number of employees to pick up plus one to include the office), how many cars we can use (which is _numberOfCars - the count of the driver names) and the index of the start & end locations of the driver – referred to as the “depo” (which is the node at index 0).
private void SetTravelDistances(RoutingModel routing, RoutingIndexManager manager)
{
var transitCallbackIndex = routing.RegisterTransitCallback((fromIndex, toIndex) =>
{
// Convert from routing variable Index to distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return _model.DistanceMatrix[fromNode, toNode];
});
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
}
We register a transit call back so that every time Google OR-Tools is deciding whether to travel to a node, it can evaluate the distance between these nodes. For example, if fromNode is 0 and toNode is 1, it’ll give you the distance from the office to employee 1. If you put a breakpoint in the code, it will be hit many times, as the model is deciding which nodes to insert at every point of its journey.
SetAreCostEvaluatorOfAllVehicles : An important part of the code, that is telling us the cost to go from employee A to employee B. You can have different TransitCallbacks going on at the same time, depending on whether you want to measure distance, time or anything else. On top of this, you can also set further constraints, like the number of passenger seats available in the vehicle (i.e., the maximum number of nodes a driver can visit), which will provide an accurate evaluation of the journey details.
So, once we’ve set the travel distance and specified the distance between two nodes, we then call SolveModel to obtain a solution.
private static Assignment SolveModel(RoutingModel routing)
{
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
searchParameters.LocalSearchMetaheuristic = LocalSearchMetaheuristic.Types.Value.GuidedLocalSearch;
searchParameters.TimeLimit = new Duration {Seconds = 1};
Assignment solution = routing.SolveWithParameters(searchParameters);
return solution;
}
We define a lot of Google OR-Tools’ specific code using the DefaultRoutingSearchParameters, this naming convention that has been provided for us here. The FirstSolutionStrategy is the cheapest arc, i.e. the cheapest way to get to all of the nodes.
With Google OR-Tools, you are given a lot of flexibility in that you can basically tell the programme how to solve your problem. With that being said, in this context they advise that you pass in GuidedLocalSearch. A quirk of GuidedLocalSearch is that it never terminates; it just goes on forever looking for solutions and does not keep track of whether it’s found a certain solution or not.
What this means is that you can tell it to exit after however long you want; most optimal solutions are found in under one minute.
Another quirk of Google OR-Tools is that if it can’t find a solution, the returned Assignment will be null. For example, if you were to put a negative distance between two employees’ locations; OR-tools would return null. Sometimes OR-Tools returns something with a status of ‘model invalid’ too (for example if you provided no drivers for it to use).
private Dictionary<string, string[]> GetAssignments(RoutingModel routing, RoutingIndexManager manager, Assignment solution)
GetAssignments is the manual code which translates the assignment object into an object that we can use and asserts for every car, driver, etc.
Index = solution.Value(routing.NextVar(index));
The even more important part of this code is solution.Value which says ‘I have a variable that has been solved by Google OR-Tools, give me the value of it’. This value is set to the Index of the node chosen text. This is the first model implemented and will ensure that everyone is picked up on the way back to the office. Read part 2 to find out how we optimise the issue of cooking the pizzas...
Audacia is a software development company based in the UK, headquartered in Leeds. View more technical insights from our teams of consultants, business analysts, developers and testers on our technology insights blog.
Technology Insights

